ラボ実験2：計数統計とエラー予測

目的：

1. 放射線の統計的性質を理解します。
2. 統計量を計算します。
3. 取得したデータセットの不確かさ分析を行います。

必要な機器：

理論の概要：

放射性壊変はランダムなプロセスです。実験では、データの統計的性質により、得られるカウント数は変動します。このような測定を何度も繰り返した結果を記述する分布関数を予測することができます。

放射線計数で使用される一般的な3つの統計モデルは以下の通りです。

1. 二項分布
2. ポアソン分布
3. ガウシアン分布

統計分析

あらゆる統計分布の基準は、真の値と任意の測定値の差です。多くの場合、真の値は、測定値の集合から実験的に決定され、標準偏差と実験平均の両方を含みます。N個の独立した測定値の集合の実験平均は、次式で表すことができます。

ここでは、

Nを測定値の総数、X_iを任意の測定値とします。

一方、サンプルの分散は次式で表されます。

サンプル分散の平方根はサンプルの標準偏差であり、測定値の不確実性のレベルを定量化するためによく使用されます。

不確実性伝播

3つの独立変数x、y、zが不確実性σ_x 、σ_y 、σ_zを用いて直接測定されると仮定しましょう。

xとy間の測定されたカウント数の差uは、次式で表すことができます。

伝播測定の不確かさは次式のようになります。

計数の合計についても同様です。計数xとzの和は次式で表すことができます。

xとzの和に対する伝播測定の不確かさは次式のようになります。

ポアソン分布

ポアソン分布は、「個々の試験の成功確率が一定で小さいことを特徴」としています（77ページの参考文献3を参照）。一定の時間間隔で原子核崩壊が起こる確率を考えます。

材料の半減期が小さい場合、確率は上がるのか、それとも下がるのか？

ポアソン変動の対象となる1つの測定値に対する予想標準偏差は次式のとおりです。

（平均値は標準値とほぼ同じであるため）。データがポアソンモデルに適合する場合、実験で測定された分散は、計算された分散とほぼ同じになります。

カイ二乗分析

実験者は、常に次のように考えるようにしましょう。取得したデータは真実なのか、それとも何らかの外的要因の影響を受けているのか？データの良し悪しをチェックするために最も頻繁に使用される検定の一つが、χ2（カイ二乗）検定です。

ここでは、

X_iとX_eは、N個の測定値とN個の測定値の平均値を表します。

カイ二乗検定を評価するために、ポアソン分布に適合するデータについて期待される結果は、N–1に等しくなります。N–1からの偏差が大きければ大きいほど、期待される挙動から得られるデータのばらつきも大きくなります。 偏差が大きい場合、実験者は予想された結果を見直すか、実験データを見直すか、実験についてさらに調査を行う可能性があります。

実験2の手引き：

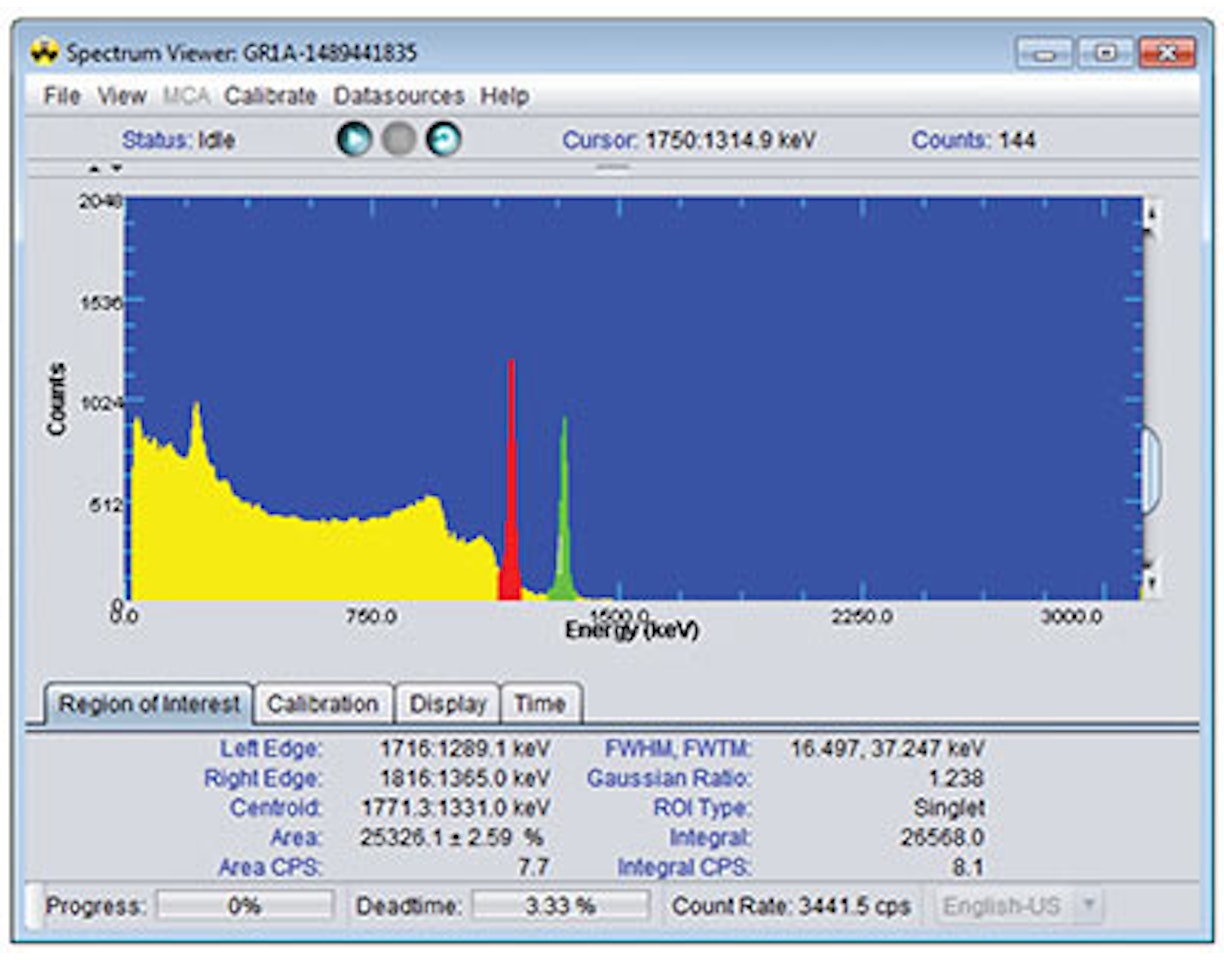
1. OspreyとNaI検出器を接続し、実験1の推奨事項に従って設定します。¹³⁷Cs光電ピークがスペクトルの中央になるようにゲインを調整します。

2. NaI検出器により20セットのバックグラウンド測定値を記録します。各測定でProSpectのPHA取得プリセットのライブ時間を30秒に設定します。

3. このデータを取得したら、検出器の近くに¹³⁷Cs線源を設置します。線源がある状態で測定を繰り返します。

警告：開始後は検出器や線源のジオメトリーを変更しないでください。

4. ステップ2と3のそれぞれのデータセットについて、方程式2-1と2-2を使用し、スペクトルの総カウント数を用いて、実験平均（X_e）とサンプル分散（σ²）を計算します。

5. 各ケースの単一測定値の不確実性を計算します。この場合、その不確実性は、σ_i = X_iで示されます。

6. ステップ4と5の結果から、そのデータがポアソンモデルのデータに適合するかどうかについてコメントします。

7. ステップ2と3で取得したデータセットにχ2検定を適用します。

8. 方程式2-4を用いて、正味計数（平均線源計数から平均バックグラウンド計数を差し引いたもの）の標準偏差を計算します。