Expérience de laboratoire 11 : Calibration de l'efficacité mathématique

Objectif :

1. Démontrer comment utiliser la modélisation mathématique pour effectuer des calibrations d'efficacité et vérifier le résultat avec une source radioactive.

Équipement requis :

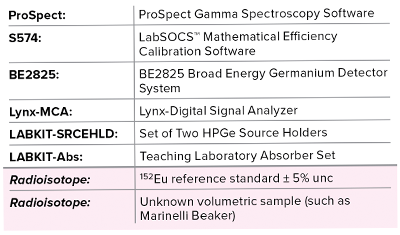
Aperçu théorique :

Mesurer l'efficacité avec les sources nécessite un inventaire des sources qui corresponde aux géométries mesurées. Il est possible d'acquérir des sources de géométries de laboratoire communes, par exemple des solutions liquides pour les béchers ou des matrices époxy pour les béchers Marinelli. Cependant, il y a des géométries qui ne sont pas pratiques à fabriquer avec les sources, ou il peut y avoir des cas de sources de forme impaire qui ne seront mesurées que quelques fois. Quelquefois, les paramètres de l'échantillon sont différents de la source de calibration. Dans tous ces cas, des calibrations mathématiques peuvent être utilisées à la place, telles que la simulation Monte-Carlo (par exemple code de transport de N-Particle eXtended [MCNPX]) ou la méthodologie LabSOCS (logiciel de calibration sans laboratoire SOurceless) et ISOCS (systèmes de comptage d'objets In-Situ). L'interaction des photons avec la matière et ses sections efficaces sont bien documentées et tabulées pour tous les atomes naturels pour une plage d'énergies élargie. Voir la figure 11-1 et l'expérience 3.

Utilisation de l'équation :

L'atténuation des photons traversant un matériau de longueur x peut être calculée. À partir des sections transversales, des densités, de la composition atomique et de la longueur du trajet à travers tous les matériaux entre le point et le détecteur, on peut calculer l'atténuation des photons d'une énergie donnée provenant d'un point dans l'espace et dirigés vers un point du détecteur. Cette méthode, utilisée par le logiciel LabSOCS et ISOCS, est appelée lancer de rayon. Afin de mesurer l'efficacité du point, il est également nécessaire de savoir l'efficacité du point sans les matériaux, c'est-à-dire dans le vide. Avec tous ces paramètres, il est possible de calcuter l'efficacité pour ce point dans le scénario de mesure. Des points sont générés uniformément dans la partie radioactive de la géométrie et l'efficacité est calculée pour chacun de ces points. L'efficacité pour l'échantillon entier est la moyenne de ces points. Une fois les points supplémentaires générés, l'efficacité de l'échantillon converge et le calcul est terminé.

L'un des nombreux avantages de la modélisation mathématique est qu'il est facile d'affiner le modèle si l'échantillon n'est pas en accord avec la géométrie modélisée. Par exemple, si la hauteur de remplissage d'un bécher n'est pas la même que la hauteur de remplissage modélisée, le modèle peut changer pour tenir compte de la différence. Cela diffère d'une calibration basée sur la source, où la source de référence ou la géométrie de mesure de l'échantillon doit être physiquement modifiée, et ou l'incertitude dans l'activité de l'échantillon doit être augmentée de manière significative pour tenir compte de la polarisation introduite par l'écart entre la source de référence et l'échantillon. Tous les autres paramètres peuvent être modifiés de manière similaire pour les efficacités modélisées.

Figure 11-1 : Coefficient d'atténuation linéaire de l'interaction de photons dans le fer en fonction de l'énergie.

Introduction au logiciel LabSOCS (efficacité mathématique)

Le logiciel LabSOCS et ISOCS nécessite que le détecteur à utiliser ait été caractérisé par le fabricant du détecteur. La caractérisation est basée sur des mesures de haute précision et une optimisation de la simulation. Cela fournit les efficacités du point de vide uniques à chaque détecteur, et le logiciel de calibration détermine ensuite la correction d'atténuation pour la géométrie de mesure spécifique. Le logiciel LabSOCS et ISOCS comprend un certain nombre de modèles de source à choisir, tels que la source ponctuelle, la sphère, le cylindre, le bécher, la boîte, etc.

L'utilisateur sélectionne une géométrie de modèle, détermine les dimensions physiques pertinentes et identifie une gamme d'énergies pour calcuter les valeurs d'efficacité. La figure 11-2 montre une image des différentes géométries de source disponibles dans le logiciel LabSOCS. Le tableau 11-1 montre une liste typique des énergies et des efficacités du logiciel LabSOCS, tandis que la figure 11-3 montre un graphique d'efficacité typique basé sur les valeurs dans le tableau. Référez-vous aux références 9 et 10 de la page 77 pour plus d'informations sur la mise en place et l'exécution des géométries LabSOCS.

Figure 11-2 : Sélection des modèles de géométrie d'échantillon LabSOCS.

Pour qu'une calibration de l'efficacité soit précise, il est essentiel que la géométrie utilisée pour générer l'efficacité soit en accord avec la géométrie du nombre d'échantillons. Cela signifie qu'en modélisation mathématique, le modèle généré doit refléter fidèlement l'échantillon qui a été mesuré. Il comprend les dimensions du détecteur, de l'échantillon, des absorbeurs ou des collimateurs, la composition du matériau et la densité. Il faut prendre des précautions supplémentaires pour modéliser avec précision les matériaux entre la source et le détecteur et l'emplacement de la source et des matériaux (surtout à proximité du détecteur où l'efficacité est sensible aux petits changements d'emplacement). De nombreux béchers couramment utilisés n'ont pas de fond plat, mais un fond légèrement incurvé. Si l'échantillon est positionné directement sur le capuchon d'extrémité et le fond du bécher n'est pas modélisé avec précision, cela peut conduire à une polarisation significative dans l'efficacité calculée, et donc affeter le résultat final de la mesure. Les parties de l'échantillon qui ne sont pas directement entre la partie radioactive de la géométrie et le cristal du détecteur n'influencent pas l'efficacité de pic et ne nécessitent donc pas autant d'attention.

Tableau 11-1 : Efficacités calculées par LabSOCS pour une source ponctuelle située à 20 cm de la surface des détecteurs NaI 2x2.

Figure 11-3 : Efficacité modélisée pour des détecteurs NaI 2x2 avec une source ponctuelle située à 20 cm du capuchon d'extrémité.

Guide de l'expérience 11 :

Exercice 1

1. À l'aide du logiciel LabSOCS, répliquez la mise en place expérimentale du détecteur de germanium de l'expérience 8 et extrayez les valeurs d'efficacité.

2. Tracez ces derniers dans Excel ou une autre application graphique.

3. Comparez la courbe d'efficacité modélisée avec la courbe d'efficacité mesurée de l'expérience 8. Commentez les différences.

4. Estimez les incertitudes dans l'efficacité mesurée (incertitude statistique et incertitude des certificats). Regardez le manuel LabSOCS pour les incertitudes modélisées. Les efficacités mesurées et calculées concordent-elles dans les limites des incertitudes ? Si non, mesurez à nouveau les dimensions de l'échantillon et affinez le modèle.

Exercice 2

1. Assurez-vous que le DSA Lynx II (avec le détecteur HPGe branché) est relié au PC de mesure directement, ou via votre réseau local.

2. À l'aide du porte-source réglable, placez la norme de référence ¹⁵² Eu à une distance d'environ 20 cm du capuchon d'extrémité du détecteur de germanium haute pureté. Enregistrez cette distance. Retirez tout matériau entre la source et le détecteur avant de compter. Placez l'un des matériaux du kit d'absorbeur entre la source et le détecteur.

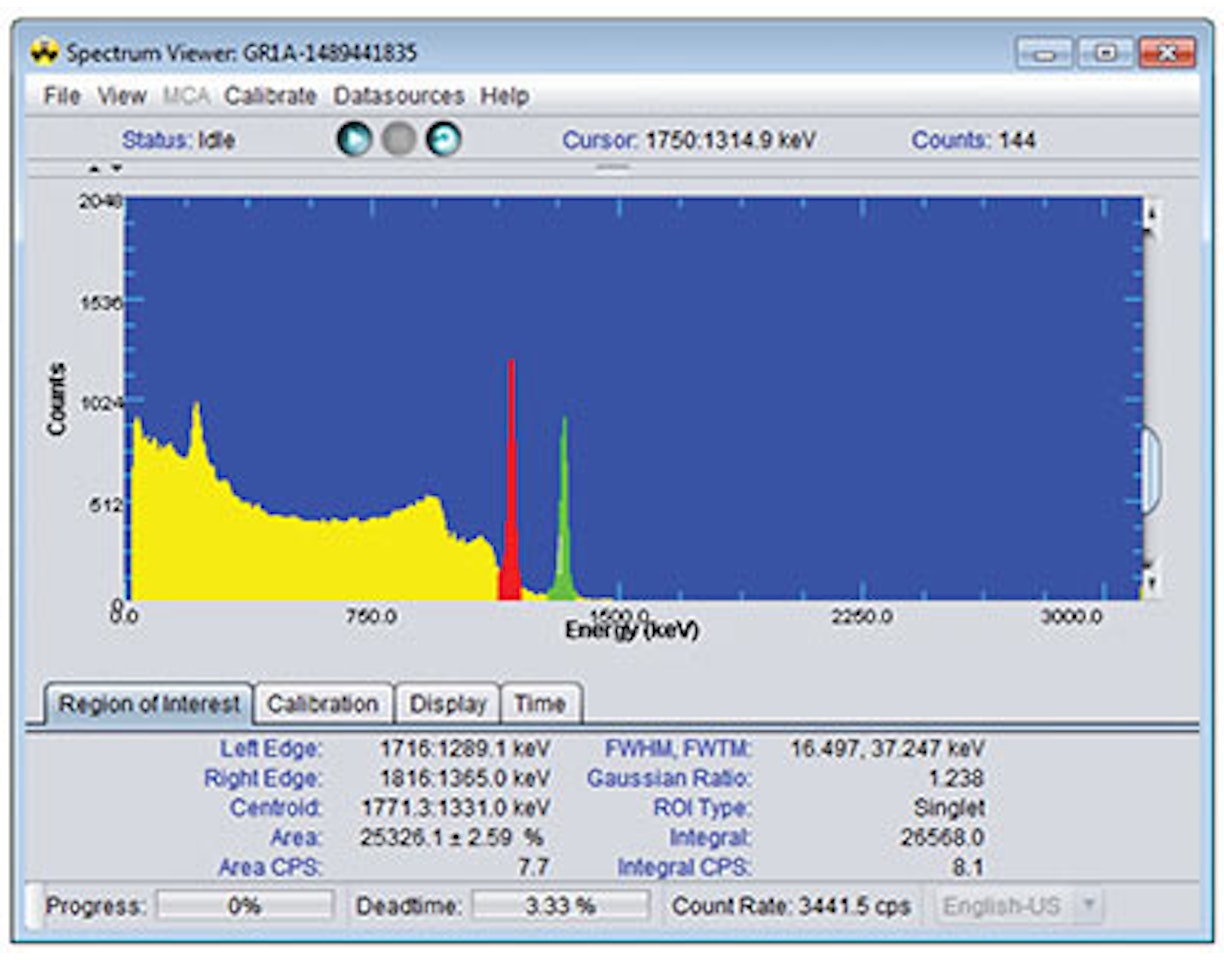
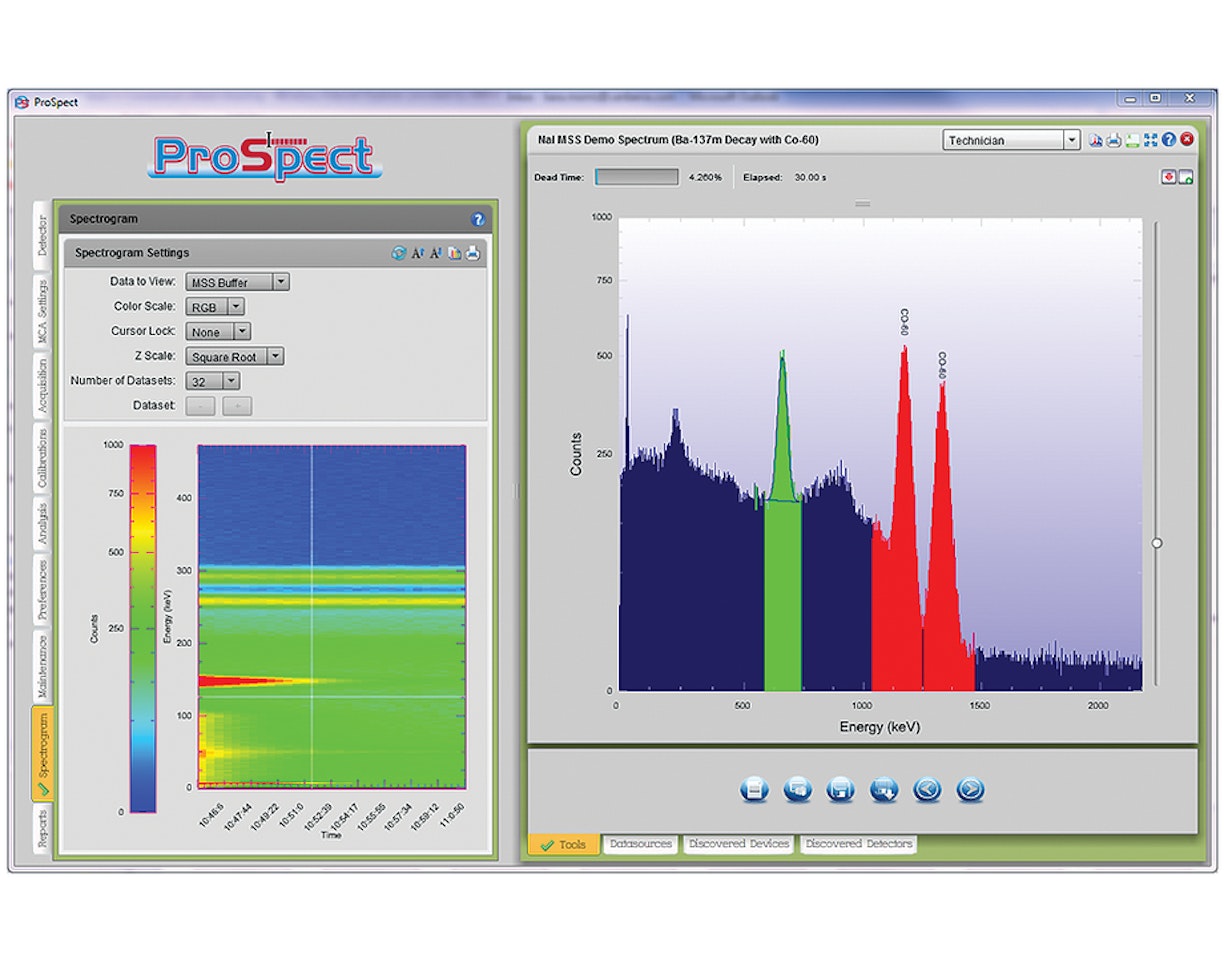
3. Ouvrez le logiciel de spectrométrie gamma ProSpect et connectez au DSA Lynx II.

4. Personnalisez les paramètres de l'analyseur multicanal comme recommandé dans l'expérience 7.

5. Utilisez le logiciel pour appliquer la polarisation recommandée du détecteur au détecteur HPGe.

6. Réglez le gain de conversion de l'analyse d'amplitude des impulsions à 32 768 canaux

7. Ajustez le gain grossier et le gain fin de l'analyseur multicanal de manière à ce que le pic de 1408 keV soit visible dans la partie supérieure du spectre.

8. Collectez des données, en veillant à ce qu'au moins 10 000 comptages soient réalisés dans plusieurs des pics principaux du spectre. Utilisez le tableur pour calcuter les coefficients de calibration de l'énergie. Entrez ces derniers dans le logiciel ProSpect à l'aide de l'onglet Calibration de l'énergie.

9. Mesurez la zone de pic nette et l'incertitude pour chacun des principaux pics. Calculez le rapport des taux de comptage pour chaque pic aux taux de comptage pour les données collectées dans l'expérience 8.

10. Modélisez la mise en place de l'expérience de l'étape 2 dans le compositeur de géométrie LabSOCS et extrayez les valeurs d'efficacité. Calculez le rapport entre les valeurs d'efficacité pour cette géométrie et les valeurs d'efficacité extraites dans l'exercice 1. Quelle est la comparaison avec les ratios calculés à l'étape 9 ?

Exercice 3

1. Placez un échantillon volumique d'activité non identifiée sur le détecteur de germanium.

2. Comptez l'échantillon pendant suffisamment de temps pour collecter 10 000 comptages dans plusieurs pics significatifs. Mesurez la zone de pic nette et l'incertitude pour chacun des principaux pics, et identifiez les nucléides candidats dans l'échantillon.

3. À l'aide du compositeur de géométrie LabSOCS, identifiez un modèle qui est compatible avec la géométrie de mesure. Mesurez les paramètres physiques et entrez-les dans le logiciel LabSOCS. Extrayez les résultats d'efficacité.

4. Utilisez les résultats d'efficacité du LabSOCS, le comptage de la zone de pic et les intensités de photons identifiées pour les nucléides candidats et calculez l'activité des nucléides dans l'échantillon. Discutez des sources possibles d'erreur et d'incertitude.

Exercice 4

1. Dans le compositeur de géométrie LabSOCS, créez un modèle d'un échantillon volumique (tel que le modèle de bécher simple) sur le capuchon de bout du détecteur ou utilisez celui de l'exercice précédent et calculez l'efficacité pour une gamme d'énergies de photons.

2. Calculez l'efficacité du même échantillon à l'étape 1, mais à une distance de 10 cm du détecteur.

3. Calculez l'efficacité du même échantillon à l'étape 1, mais à une distance de 10 cm du détecteur avec un absorbeur entre l'échantillon et le détecteur.

4. Comparez les trois efficacités modélisées aux deux efficacités mesurées pour un pic de faible, moyenne et haute énergie. Pour les différentes énergies, quel est le paramètre le plus important, la distance source-détecteur ou les matériaux entre la source et le détecteur ?

5. Dans l'un des modèles créés, diminuez la hauteur de remplissage de l'échantillon de 50 % et calculez les efficacités. Comparez ensuite le avec le modèle d'origine pour un pic de haute, moyenne et basse énergie. Pour quelle énergie l'efficacité change-t-elle le plus ? Expliquez le résultat.