Expérience de laboratoire 2 : statistiques de comptage et prédiction des erreurs
- Imprimer
Objectif :
- Comprendre la nature statistique de la radiation.
- Calculer des quantités statistiques.
- Effectuer une analyse d'incertitude sur un ensemble de données acquises.
Équipement requis :

Aperçu théorique :
La décroissance de la radioactivité est un processus aléatoire. Lors d'une expérience, le nombre de comptages obtenus fluctuera en raison de la nature statistique des données. On peut prédire la fonction de distribution qui décrit les résultats de nombreuses mesures répétées.
Les trois modèles statistiques courants qui sont utilisés dans le comptage nucléaire sont :
- La distribution binomiale
- La distribution de Poisson
- La distribution gaussienne
Analyse statistique
La base de toute distribution statistique est la variation d'une mesure donnée par rapport à la valeur réelle. La valeur réelle est souvent déterminée expérimentalement à partir d'un ensemble de mesures et comprend à la fois la moyenne expérimentale et l'écart-type. La moyenne expérimentale pour un ensemble de N mesures indépendantes peut être exprimée comme suit :

Où :
N est le nombre total de mesures et Xi est la valeur d'une mesure donnée.
Pendant ce temps, la variance de l'échantillon est exprimée comme suit :

La racine carrée de la variance de l'échantillon est l'écart-type de l'échantillon, qui est souvent utilisé pour quantifier le niveau d'incertitude d'une valeur mesurée.
Propagation des incertitudes
Supposons que trois variables indépendantes x, y, z sont directement mesurées avec des incertitudes σx , σy , σz.
La différence dans le nombre de comptages mesurés, u, entre x et y peut être exprimée comme suit :

L'incertitude de mesure propagée devient :

Il en va de même pour la somme des comptages. La somme des comptages x et z peut être exprimée comme suit :

L'incertitude de mesure propagée pour la somme de x et z est :

La distribution de Poisson
La distribution de Poisson est « caractérisée par une probabilité de succès constante et faible pour chaque essai individuel » (se référer à la référence 3 de la page 77). Considérons la probabilité qu'une désintégration nucléaire se produise dans un certain intervalle de temps.
La probabilité augmente-t-elle ou diminue si la période radioactive du matériau est petite ?
L'écart-type attendu pour une mesure soumise à des fluctuations de Poisson est :

(Comme la valeur moyenne est approximativement la même que toute valeur typique). Si les données correspondent au modèle de Poisson, la variance mesurée expérimentalement doit être approximativement la même que la variance calculée.
Test du chi carré
Un expérimentateur devrait toujours poser la question : les données obtenues sont-elles vraies, ou sont-elles affectées par des perturbations externes ? L'un des tests les plus fréquemment utilisés pour vérifier la bonne qualité des données est le test χ 2 (chi carré) :

Où :
Xi et Xe représentent les mesures N individuelles et la moyenne des mesures N.
Pour évaluer le test de chi carré, le résultat attendu pour les données correspondant à une distribution de Poisson est équivalent à N-1. Plus l'écart par rapport à N-1 est important, plus la variation des données du comportement attendu est importante. Si l'écart est important, l'expérimentateur peut être amené à approfondir l'expérience, qu'il s'agisse de revoir le résultat attendu ou les données expérimentales.
Guide de l'expérience 2 :
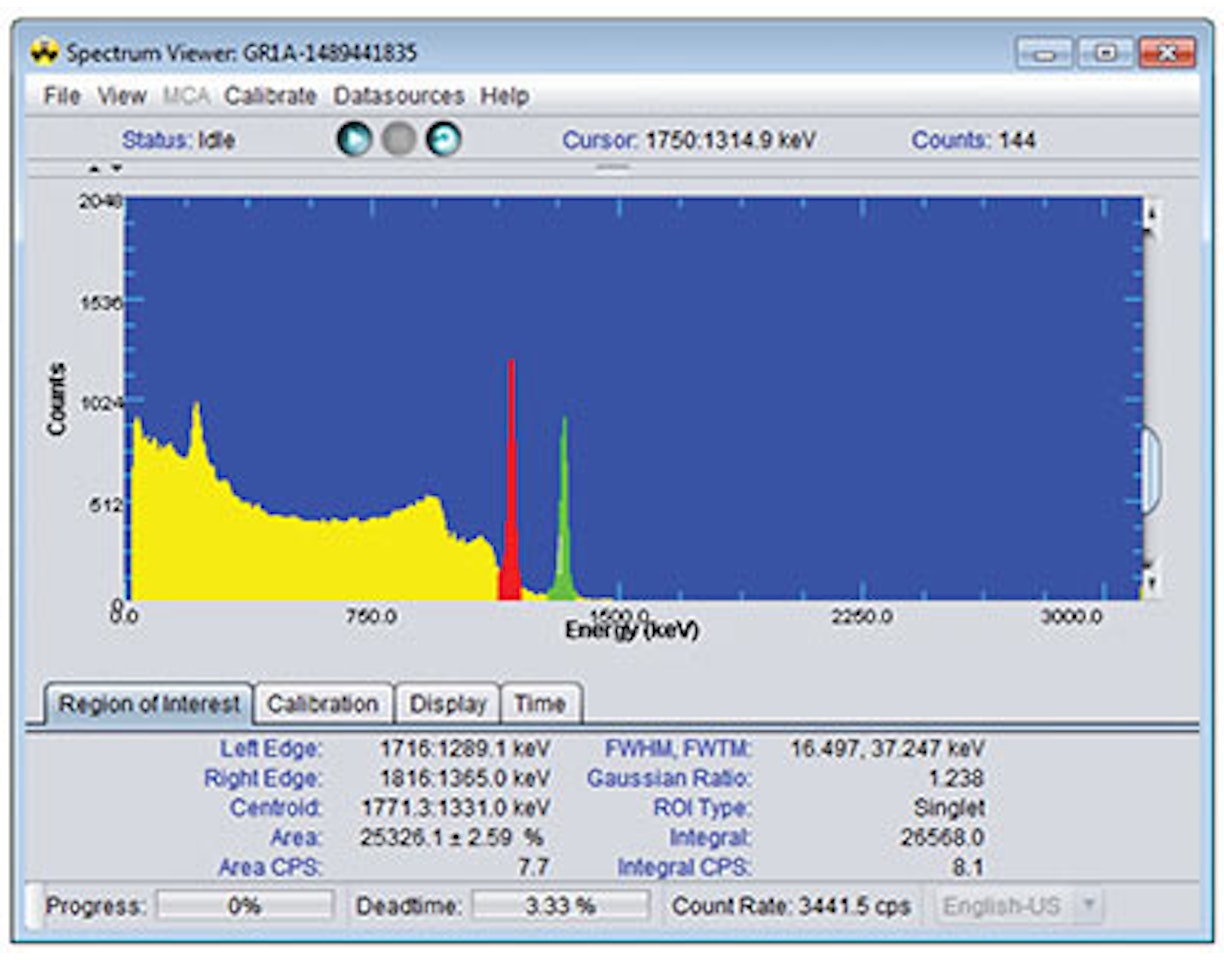
1. Reliez le détecteur Osprey et le détecteur NaI et configurez-les comme recommandé dans l'expérience 1. Ajustez le gain de sorte que le photopeak de 137 Cs soit au centre du spectre.
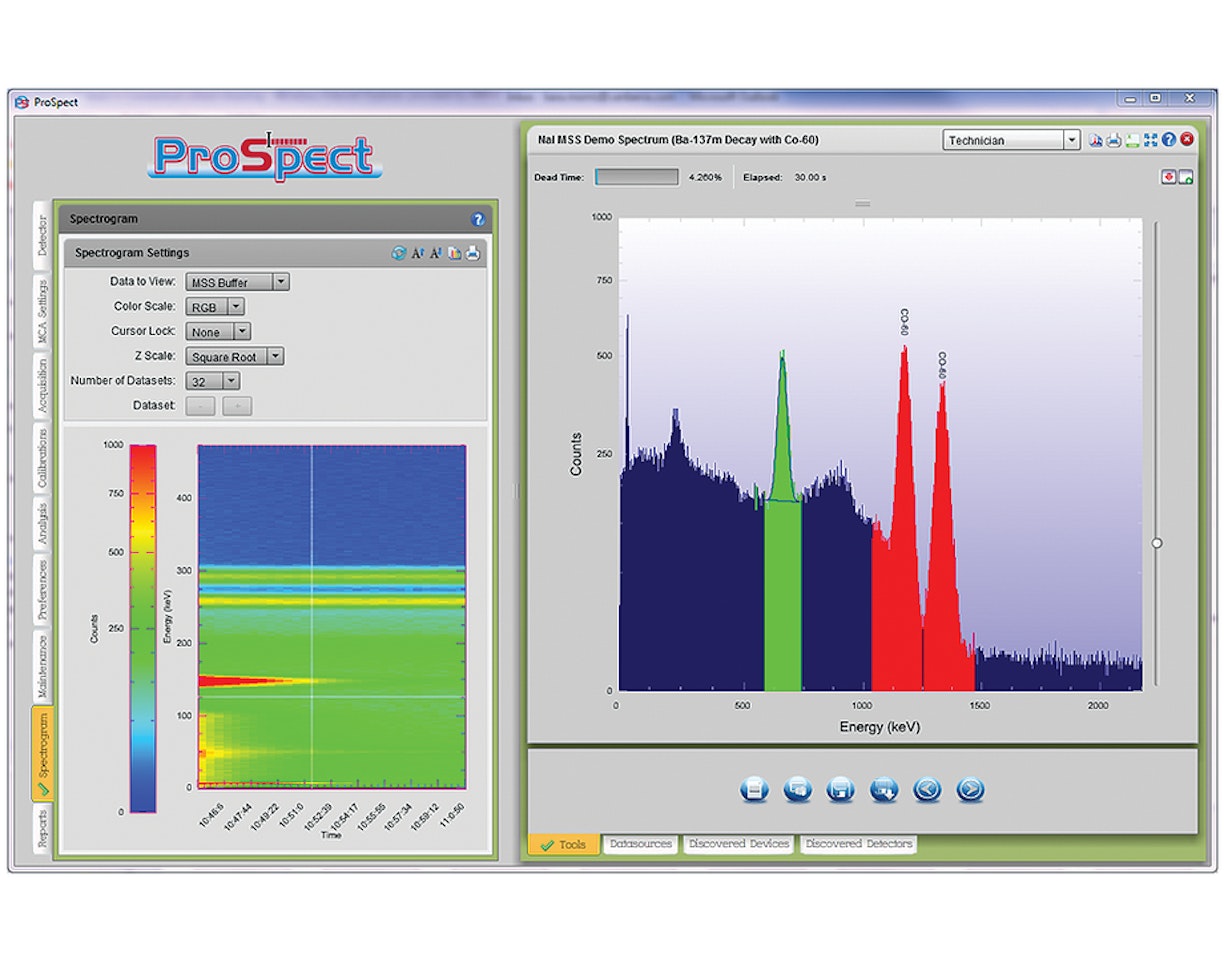
2. Enregistrez un ensemble de 20 mesures de bruit de fond avec un détecteur NaI. Dans ProSpect, réglez la durée de vie prédéfinie de l'acquisition PHA sur 30 secondes pour chaque mesure.
3. Une fois ces données prises, placez une source 137 Cs près du détecteur. Répétez les mesures avec la source présente.
Attention : ne modifiez pas la géométrie du détecteur et de la source une fois que vous démarrez.
4. Pour chaque ensemble de données des étapes 2 et 3, calculez la moyenne expérimentale (Xe) et la variance de l'échantillon (σ2) à l'aide des équations 2 - 1 et 2 - 2, à l'aide des comptages totaux dans le spectre.
5. Calculez l'incertitude d'une mesure unique dans chaque cas qui, dans ce cas, est obtenue comme suit : σi = Xi
6. À partir des résultats des étapes 4 et 5, commentez si les données correspondent au modèle de données de Poisson.
7. Appliquez le test χ 2 aux ensembles de données obtenus aux étapes 2 et 3. Commentez les résultats.
8. Calculez l'écart-type sur les comptages nets (le comptage de source moyen moins le comptage de bruit de fond moyen) à l'aide de l'équation 2 - 4.