Laborversuch 12: Echte Zufallssummenbildung

Zweck:
- Zur Demonstrierung wahrer Zufallssummen.
Erforderliche Ausrüstung:
Theoretische Übersicht:
Gamma-Gamma-Koinzidenzen
Viele gebräuchliche Nuklide geben bei ein und demselben Zerfall zwei oder mehr Photonen ab, was oft als Kaskade bezeichnet wird. Der anfängliche Zerfall (es könnte sich um α, β-, β+ oder Elektroneneinfang handeln) erzeugt im Tochterkern einen erregten Zustand. Dieser Zustand zerfällt durch Photonenemission oder interne Umwandlung in einen weniger erregten Zustand des Kerns (es könnte der Grundzustand sein).
Abbildung 12-1 zeigt das Zerfallsschema von 60Co, in dem die aufeinanderfolgenden Zerfälle der angeregten Zustände zu sehen sind

Abbildung 12-1: Das Zerfallsschema des 60Co-Zerfalls.

Abbildung 12-2: Ein Zerfall, bei dem zwei Photonen abgestrahlt werden und beide Energie in den Detektor abgeben.

Abbildung 12-3: Zerfallsschema zum Nachweis des „Aufsummierugs“-Effekts für Energie EC.„“
Die typische Lebensdauer angeregter Zustände in einem Kern liegt im Pikosekundenbereich. Die typische Reaktionszeit eines Detektors, d. h. die Mindestzeit zwischen zwei Photonenereignissen, die vom Detektor benötigt wird, um diese als zwei separate Ereignisse zu erkennen, liegt in der Größenordnung von Mikrosekunden. Man beachte, dass dies um mehrere Größenordnungen länger ist als die typische Lebensdauer der Anregungszustände. Bei Zerfällen, bei denen mehr als ein Photon abgestrahlt wird, besteht eine hohe Wahrscheinlichkeit, dass mehrere Photonen mit dem Detektor zusammenwirken und dort Energie abgeben. Da die Zeit zwischen den Photonenemissionen viel kürzer ist als die Ansprechzeit des Detektors, kann dieser die Photonen nicht als separate Ereignisse unterscheiden und es wird nur ein Impuls erzeugt, welcher der Summe der einzelnen abgegebenen Energien entspricht. Abbildung 12-2 zeigt ein Beispiel für einen Zerfall, bei dem zwei Photonen freigesetzt werden und beide im Detektor innerhalb der Detektorauflösung Energie abgeben. Dieses Ereignis wird als wahre Zufallssummenbildung oder Kaskadensummenbildung bezeichnet. Zwei Fälle verlangen besondere Aufmerksamkeit:
1. Summing Out Hierbei legt eines der Photonen seine gesamte Energie im Detektor ab (z. B. der Gammastrahl von 1173 keV in Abb. 12-1) und das andere Photon (z. B. der Gammastrahl von 1332 keV) legt einen Teil oder die gesamte Energie im Detektor ab. Dies verschiebt eine Zählung vom Full Energy Peak des ersten Photons (in diesem Beispiel bei 1173 keV) zu einer höheren Energie im Spektrum. Dadurch verringert sich die Zählrate des ersten Photons verglichen mit dem Nachweis nur eines einzelnen Photons. Dieses Phänomen wird Summing Out genannt.
2. Summing In Dieser Effekt ist von Bedeutung, wenn die interessierende Gammaenergie gleich der Summe der Energie von zwei anderen Gammastrahlen im Zerfallsschema ist, wie im Beispiel in Abbildung 12-3. Hier führt die Summenbildung zwischen Gammastrahlen der Energie EA und EB zu einer Erhöhung der Zählrate des Peaks bei Energie EC. Das wird als Summing In bezeichnet.
Gammastrahlen-Koinzidenz
Es gibt zwei Möglichkeiten, wie Röntgenstrahlen erzeugt werden können, sodass sie zur wahren Zufallssummenbildung beitragen.
1. Elektroneneinfang Hier wird eines der eng aneinander gebundenen Elektronen eingefangen, wodurch auf einer der inneren Elektronenhüllen eine Leerstelle entsteht. Elektronen aus der äußeren Hülle füllen die Leerstelle in der inneren Hülle und senden nachweisbare Röntgenstrahlung aus. Da diese Röntgenstrahlen aus dem anfänglichen Zerfall entstehen, kann jedes vom Tochterkern abgestrahlte Photon in Übereinstimmung mit den Röntgenstrahlen nachgewiesen werden (einschließlich der Fälle, in denen ein einzelnes Photon abgestrahlt wird). Dies ist ein Beispiel für die Summing Out.
2. Interne Umwandlung Bei der internen Umwandlung reagiert der angeregte Kern mit der Elektronenwolke um den Kern und die überschüssige Energie wird auf eines der Elektronen übertragen, das aus dem Atom ausgestoßen wird. Dadurch entsteht eine Leerstelle in einer der Elektronenhüllen, die von einem äußeren Elektron gefüllt wird und es wird ähnlich wie beim oben beschriebenen Elektroneneinfang eine Röntgenstrahlung emittiert. Dies ist auch ein Beispiel für die Summing Out.
Gammavernichtungs-Photonen-Koinzidenz
Es gibt Fälle, in denen sich die beim Zerfallsprozess (wie beim β+-Zerfall) ergebenden Photonen mit den Photonen des Tochternuklids summieren können. Beim β+-Zerfall werden Positronen freigesetzt, die im umgebenden Material verlangsamt werden, ein Elektron finden und annihilieren, wobei zwei Photonen mit einer Energie von 511 keV entstehen. Die Zeit, die es braucht, bis das Positron verlangsamt und vernichtet wird, ist kurz im Vergleich zur Reaktionszeit des Detektors. Wenn mindestens eines der Photonen aus der Annihilation Energie im Detektor abgibt und zusätzlich ein Photon im Tochterkern nachgewiesen wird, wird die Zählung vom Full Energy Peak verschoben. Dies ist ein weiterer Fall der Summing Out wie oben beschrieben.
Wahrscheinlichkeit einer wahren Zufallssummenbildung
Da die wahre Zufallssummenbildung den Nachweis von zwei Photonen aus demselben Zerfall erfordert, ist sie stark von folgenden Faktoren abhängig:
1. Die Detektionseffizienz für die Photonen, die an der Summierung teilnehmen. Dies ist eine Funktion des Detektortyps und der verwendeten Zählgeometrie. So steigt beispielsweise die Wahrscheinlichkeit, zwei Photonen als Summenereignis zu erkennen, mit zunehmender Detektorgröße und abnehmendem Abstand zwischen Quelle und Detektor.
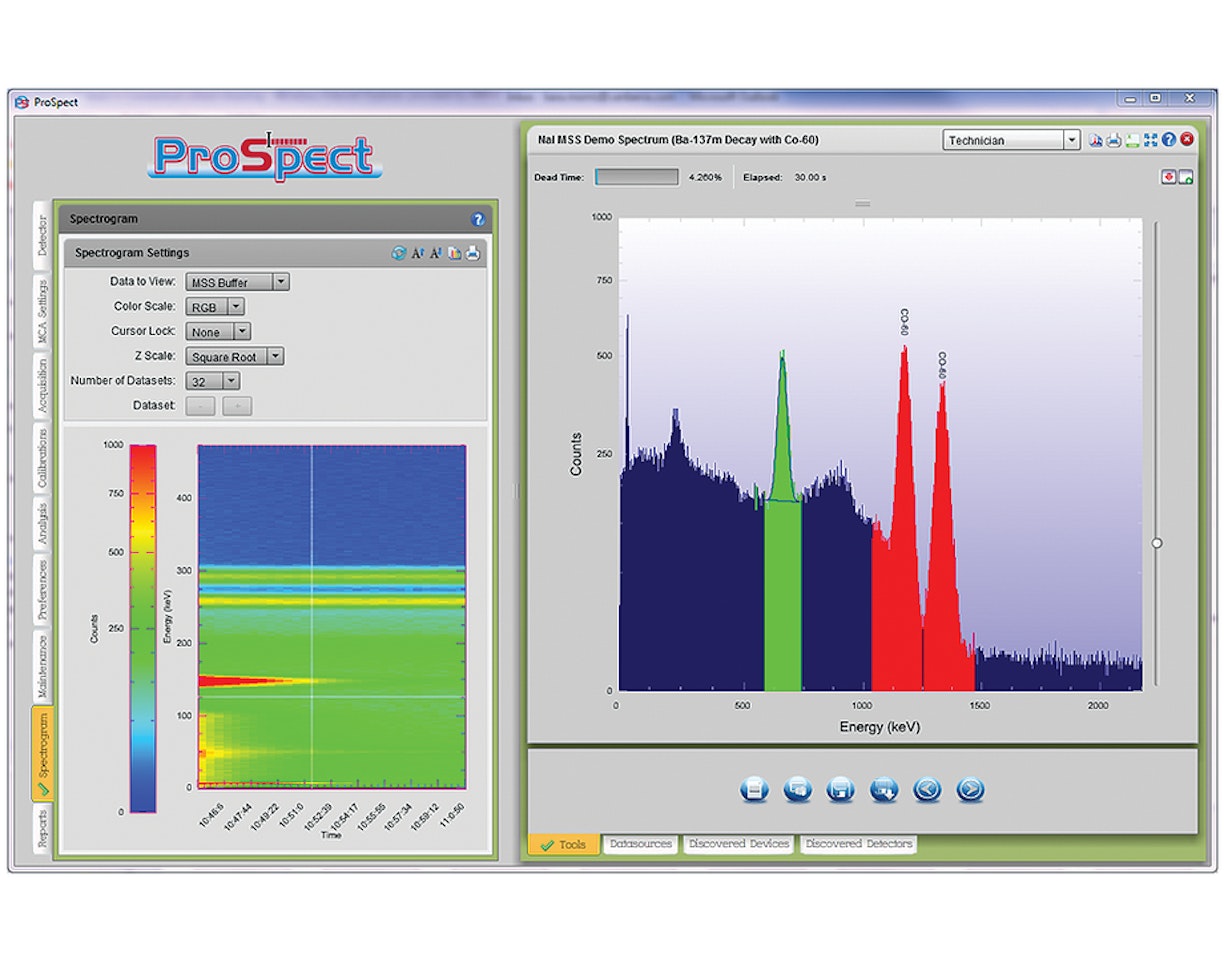
2. Das Nuklid, das gemessen wird. Genauer gesagt das Zerfallsschema des Nuklids. Früher haben wir gelernt, dass die Summenbildung und -auswertung vom Gammastrahlungs-Zerfallsschema abhängt (z. B. das Vorhandensein einer Kaskade und die Art des Zerfalls, wie interne Umwandlung oder Elektroneneinfang). Es gibt einige Kerne, die nicht betroffen sind (wie 137Cs) und andere (wie 60Co und 88Y), die erhebliche Summeneffekte aufweisen.
Konsequenzen für quellenbasierte Effizienzkalibrierungen
Die meisten handelsüblichen Multi-Gamma-Quellen enthalten Nuklide, die eine echte Zufallssummenbildung besitzen. Es ist beispielsweise üblich, 60Co und 88Y als hochenergetische, Photonen emittierende Nuklide zu verwenden und diese beiden Nuklide sind vom Summing Out betroffen. Die Verwendung von Nukliden mit Summing-Out-Effekten in engen Geometrien führt zu niedrigeren Peak-Zählraten, als wenn das Nuklid keine Summing-Out-Effekte aufweisen würde. Das Ergebnis ist, dass die Effizienz bei diesen Energien niedriger zu sein scheint als die wahre Effizienz. Wenn diese Effizienzpunkte ohne Korrektur verwendet werden, ist die berechnete Effizienz niedrig im Vergleich zur wahren Effizienz. Wenn die Effizienz zur Berechnung der Aktivität für eine summenfreie Probenmessung verwendet wird, ist das Ergebnis somit höher als die wahre Aktivität.
Konsequenzen für die Probenzählung
Bei Probenzählungen führen die Summeneffekte zu einer Verringerung der gemessenen Peak-Zählraten; die gemessenen Aktivitäten sind daher niedriger als die wahren Aktivitäten. Die Summing In hat den gegenteiligen Effekt, wobei die gemessenen Aktivitäten die wahren Aktivitäten übersteigen. Es ist anzumerken, dass Summing-out-Effekte am häufigsten sind. Außerdem ist dies der wichtigere Effekt, da die Unterschätzung der Nuklidaktivitäten Auswirkungen auf die Sicherheit haben kann.
Reduzierung des Effekts echter Zufallssummenbildung
Da die Wahrscheinlichkeit einer wahren Zufallssummenbildung von der Detektionseffizienz abhängt, kann der Effekt reduziert werden, indem die Probe vom Detektor weg bewegt wird. Die Verringerung der Gesamteffizienz des Zählsystems kann jedoch zu längeren Zählzeiten führen (zur Wahrung der Zählstatistik) und damit zu einer verringerten Produktivität bei der Probenzählung.
Wenn die Zufallssummenbildung hauptsächlich auf Röntgenstrahlen zurückzuführen ist (wie es der Fall sein kann, wenn der Kern durch Elektroneneinfang zerfällt), kann die Zufallssummenbildung durch den Einsatz eines Dämpfers reduziert werden, der die meisten niederenergetischen Photonen abschwächt. Optimal ist der Einsatz von Software, wie z. B. LabSOCS-Berechnungen, um echte Zufallssummeneffekte zu quantifizieren und zu korrigieren. Dieser Ansatz ist für alle Messgeometrien und alle häufig gemessenen Nuklide anwendbar, von denen bekannt ist, dass sie betroffen sind.
Experiment 12-Leitfaden:
Messungen
1. Stellen Sie sicher, dass der Lynx II DSA (mit angeschlossenem HPGe-Detektor) direkt oder über Ihr lokales Netzwerk mit dem Mess-PC verbunden ist.
2. Richten Sie die 137Cs-Quelle vor dem Detektor ein.
3. Öffnen Sie die Gammaspektroskopiesoftware ProSpect und stellen Sie eine Verbindung zum Lynx II DSA her.
4. Konfigurieren Sie die MCA-Einstellungen wie in Experiment 7 empfohlen.
5. Verwenden Sie die Software, um die empfohlene Detektorvorspannung auf den HPGe-Detektor anzuwenden.
6. Stellen Sie die PHA-Konvertierungsverstärkung auf 32768 Kanäle ein.
7. Stellen Sie den Verstärkungszuwachs so ein, dass der Full Energy Peak annähernd 40 % des Spektrums beträgt.
8. Führen Sie eine Energiekalibrierung durch.
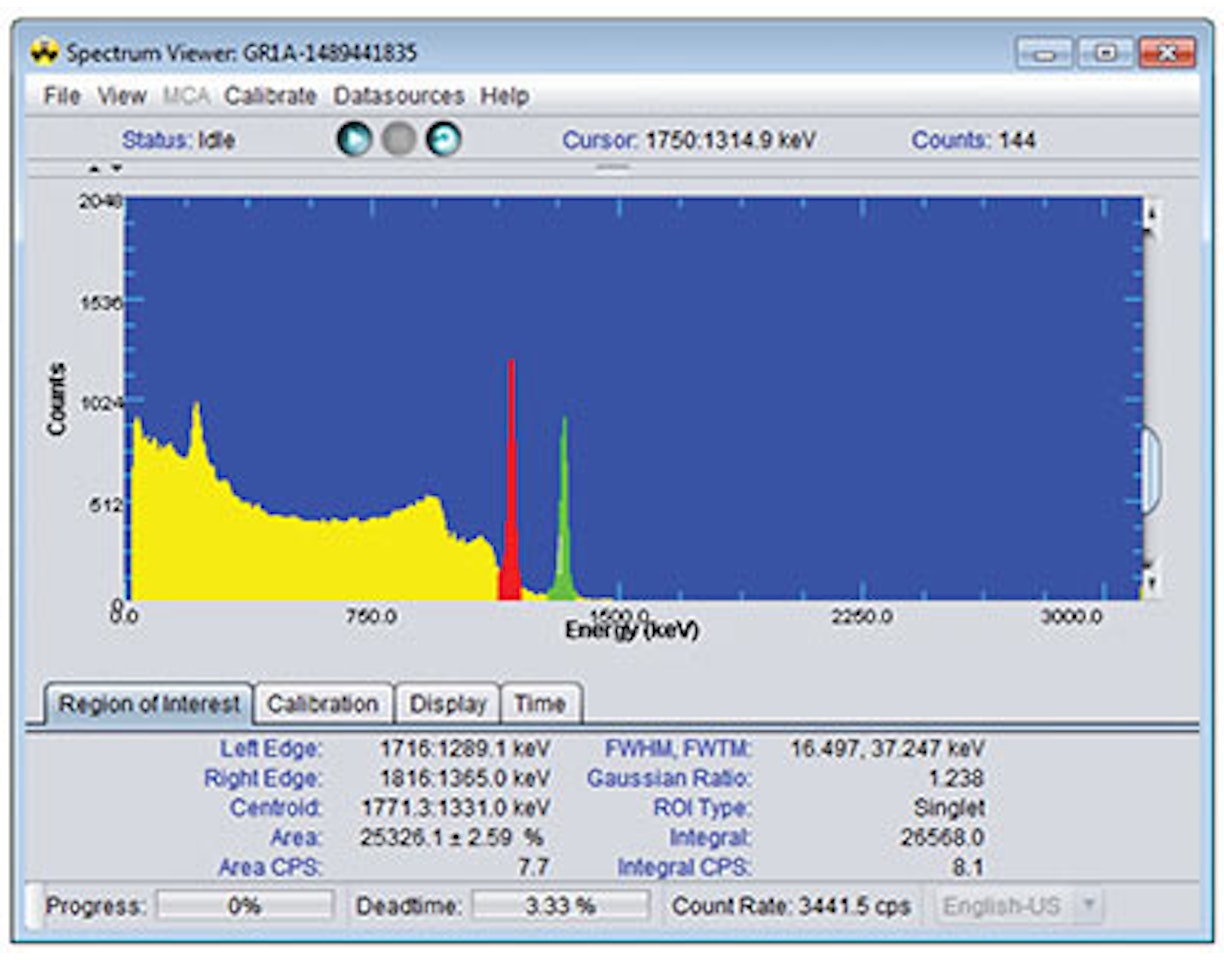
9. Bringen Sie die 137Cs-Quelle auf der Endkappe an und nehmen ein Spektrum auf (verwenden Sie eine solche Zählzeit, dass mindestens 10 000 Zählungen im Full Energy Peak vorhanden sind).
10. Notieren Sie die Anzahl der Zählungen im Full Energy Peak
11. Stellen Sie die 137Cs-Quelle 5 cm von der Quelle entfernt auf und nehmen Sie ein Spektrum auf (verwenden Sie eine solche Zählzeit, dass sich mindestens 10 000 Zählungen im Full Energy Peak befinden).
12. Notieren Sie die Anzahl der Zählungen in dem/den Full Energy Peak(s).
13. Positionieren Sie die 137Cs-Quelle 30 cm von der Quelle entfernt und erfassen Sie ein Spektrum (verwenden Sie eine solche Zählzeit, dass sich mindestens 10 000 Zählungen im Full Energy Peak befinden).
14. Notieren Sie die Anzahl der Zählungen in dem/den Full Energy Peak(s).
15. Positionieren Sie die 137Cs-Quelle auf einem dünnen Kupferblech direkt auf der Endkappe und erfassen Sie ein Spektrum (verwenden Sie eine solche Zählzeit, dass sich mindestens 10 000 Zählungen im Full Energy Peak befinden).
16. Notieren Sie die Anzahl der Zählungen in dem/den Full Energy Peak(s).
17. Wiederholen Sie Schritt 16 für eine 60Co-Quelle.
18. Wiederholen Sie Schritt 16 für eine 22Na-Quelle.
19. Wiederholen Sie Schritt 16 für eine 152Eu-Quelle.
Analyse
1. Erstellen Sie in LabSOCS Geometry Composer ein Modell der Punktquelle in den drei verschiedenen Abständen und mit dem Kupferabsorber. Berechnen Sie die Effizienzen für alle Energien, für die Peak-Bereiche berechnet wurden.
2. Anhand der Peakflächen, der Zählzeiten und der bekannten Photonenemissionsrate der Strahlenquellen (diese ist auf dem Strahlenzertifikat angegeben) werden die Wirkungsgrade für alle Strahlenquellen und Geometrien berechnet.
3. Berechnen Sie den wahren Zufallssummenfaktor (definiert als die gemessene Effizienz geteilt durch die berechnete Effizienz) für alle Quellen und Geometrien. Ein Faktor nahe 1 zeigt an, dass es keine oder eine vernachlässigbare wahre Zufallssummenbildung gibt. Ein Faktor kleiner als 1 gibt an, dass es Summing-Out-Koinzidenzen und ein Faktor größer als 1 dass es Summing-in-Koinzidenzen gibt.
4. Für jede Quelle und Geometrie erklären Sie den Wert des wahren Zufallssummenfaktors. Falls erforderlich, können Sie das Zerfallsschema in einem Buch oder online nachschlagen, beispielsweise aus dem National Nuclear Data Center im Brookhaven National Laboratory http://www.nndc.bnl.gov/nudat2/.