Laborversuch 11: Mathematische Effizienzkalibrierung

Zweck:
- Nachweis einer mathematischen Modellierung zur Durchführung von Effizienzkalibrierungen und zur Überprüfung der Ergebnisse mit einer radioaktiven Quelle.
Erforderliche Ausrüstung:
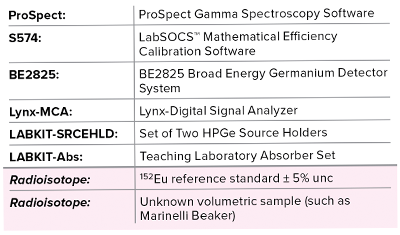
Theoretische Übersicht:
Die Effizienzmessung mit Quellen erfordert eine Bestandsaufnahme der Quellen, die den zu messenden Geometrien entspricht. Es können Ausgangsstoffe für gängige Laborgeometrien erworben werden, z. B. flüssige Lösungen für Bechergläser oder Epoxidmatrizen für Marinellibecher Es gibt jedoch Geometrien, bei denen die Herstellung von Quellen nicht praktikabel ist oder es kann Fälle geben, in denen Quellen mit ungerader Form nur wenige Male gemessen werden sollen oder in denen sich die Probenparameter von denen der Kalibrierquelle unterscheiden. In all diesen Fällen können stattdessen mathematische Kalibrierungen verwendet werden, wie z. B. Monte-Carlo-Simulationen (z. B. Monte-Carlo N-Particle eXtended [MCNPX] Transportcode) oder die LabSOCS (Laboratory SOurceless Calibration Software) und ISOCS (In-Situ Object Counting Systems) Verfahren. Die Wechselwirkung von Photonen mit Materie und ihre Wirkungsquerschnitte sind gut bekannt und für alle natürlich vorkommenden Atome für einen breiten Energiebereich aufgelistet. Siehe Abbildung 11-1 und Experiment 3.
Mit der Gleichung:

Die Dämpfung von Photonen, die ein Material der Länge x durchdringen, kann berechnet werden. Die Dämpfung von Photonen für eine bestimmte Energie, die von einem Punkt im Raum auf einen Punkt auf dem Detektor gerichtet ist, kann aus den Wirkungsquerschnitten, den Dichten, der atomaren Zusammensetzung und der Pfadlänge durch alle Materialien zwischen dem Punkt und dem Detektor berechnet werden. Diese Methode, die von der LabSOCS- und ISOCS-Software verwendet wird, wird als Raytracing bezeichnet. Um die Effizienz für den Punkt zu berechnen, ist es auch notwendig, die Effizienz des Punktes ohne die Materialien, d. h. in einem Vakuum, zu kennen. Mit all diesen Parametern kann die Effizienz für diesen Punkt im Messszenario berechnet werden. Punkte werden gleichmäßig im radioaktiven Teil der Geometrie erzeugt und die Effizienz wird für jeden dieser Punkte berechnet. Die Effizienz für die gesamte Probe ist der Durchschnitt dieser Punkte. Werden weitere Punkte erzeugt, gleicht sich die Stichprobeneffizienz an und die Berechnung ist abgeschlossen.
Einer der vielen Vorteile der mathematischen Modellierung besteht darin, dass das Modell einfach verfeinert werden kann, wenn die Probe nicht mit der modellierten Geometrie übereinstimmt. Wenn beispielsweise die Füllhöhe eines Bechers nicht mit der modellierten Füllhöhe übereinstimmt, kann das Modell geändert werden, um den Unterschied auszugleichen. Dies steht im Gegensatz zu einer quellenbasierten Kalibrierung, bei der entweder die Referenzquelle oder die Messgeometrie der Probe physikalisch verändert werden muss oder die Unsicherheit der Probenaktivität deutlich erhöht werden muss, um die durch die Diskrepanz zwischen der Referenzquelle und der Probe verursachte Verzerrung auszugleichen. Alle anderen Parameter können in ähnlicher Weise für modellierte Effizienzen geändert werden.

Abbildung 11-1: Lineare Dämpfungskoeffizienten der Photonenwechselwirkung in Eisen als Funktion der Energie.
Einführung in die LabSOCS-Software (Mathematische Effizienz)
Die LabSOCS- und ISOCS-Software setzt voraus, dass der zu verwendende Detektor vom Detektorhersteller charakterisiert wurde; die Charakterisierung basiert auf hochpräzisen Messungen und Simulationsoptimierung. So erhält man die für jeden Detektor spezifischenVakuum-Punkt-Wirkungsgrade und die Kalibrierungssoftware bestimmt dann die Dämpfungskorrektur für die betreffende Messgeometrie. Die Software LabSOCS und ISOCS enthält eine Reihe von Quellenvorlagen, aus denen Sie wählen können, z. B. Punktquellen, Kugeln, Zylinder, Becher, Kästen usw.
Der Benutzer wählt eine Vorlagegeometrie aus, bestimmt die maßgeblichen physikalischen Abmessungen und legt einen Energiebereich zur Berechnung der Effizienzwerte fest. Abbildung 11-2 zeigt ein Bild der verschiedenen in der LabSOCS-Software verfügbaren Quellengeometrien. Tabelle 11-1 zeigt eine typische Auflistung der Energien und Effizienzen der LabSOCS-Software, während Abbildung 11-3 eine typische Effizienzgrafik zeigt, die auf den Tabellenwerten basiert. Weitere Informationen zur Einrichtung und Ausführung von LabSOCS-Geometrien finden Sie unter den Verweisen 9 und 10 auf Seite 77.

Abbildung 11-2: Auswahl von LabSOCS-Probengeometrievorlagen.
Für eine genaue Effizienzkalibrierung ist es entscheidend, dass die zur Effizienzkalibrierung verwendete Geometrie mit der Geometrie der Probenzählung übereinstimmt. Für die mathematische Modellierung bedeutet dies, dass das erstellte Modell der gemessenen Probe so nahe wie möglich kommen muss. Dazu gehören die Abmaße des Detektors, der Probe, etwaige Absorber oder Kollimatoren, die Materialzusammensetzung und die Dichte. Es sollte besonders darauf geachtet werden, dass die Materialien zwischen der Quelle und dem Detektor sowie die Quellen- und Materialposition (insbesondere in der Nähe des Detektors, wo die Effizienz für geringe Positionsänderungen empfindlich ist) genau abgebildet werden. Viele häufig verwendete Bechergläser haben keine flachen Böden, sondern einen leicht gebogenen Boden. Wenn die Probe direkt auf der Endkappe positioniert wird und der Becherboden nicht genau modelliert ist, kann dies zu einer erheblichen Verzerrung der berechneten Effizienz und damit des endgültigen Messergebnisses führen. Probenteile, die nicht direkt zwischen dem radioaktiven Teil der Geometrie und dem Detektorkristall liegen, beeinflussen die Peak-Effizienz nicht und benötigen daher nicht so viel Aufmerksamkeit.
Tabelle 11-1: LabSOCS berechnete Effizienzen für eine Punktquelle in 20 cm Entfernung von der Oberfläche eines 2x2-NaI-Detektors.


Tabelle 11-3: Modellierte Effizienz für einen 2x2 NaI-Detektor mit einer Punktquelle in 20 cm Abstand von der Endkappe.
Experiment 11-Leitfaden:
Übung 1
1. Kopieren Sie mit der LabSOCS-Software den Versuchsaufbau des Germaniumdetektors aus Versuch 8 und ermitteln Sie die Effizienz
2. Zeichnen Sie diese in Excel oder einer anderen grafischen Anwendung auf.
3. Vergleichen Sie die modellierte Effizienzkurve mit der gemessenen Effizienzkurve aus Experiment 8. Kommentieren Sie alle Unterschiede.
4. Schätzen Sie die Unsicherheiten in der gemessenen Effizienz (statistische Unsicherheit und Zertifikatsunsicherheit). Für die modellierten Unsicherheiten ziehen Sie das LabSOCS-Handbuch zurate. Stimmen die gemessenen und berechneten Effizienzen innerhalb der Unsicherheiten überein? Wenn nicht, messen Sie die Abmessungen der Probe erneut und verfeinern Sie das Modell.
Übung 2
1. Stellen Sie sicher, dass der Lynx II DSA (mit angeschlossenem HPGe-Detektor) direkt oder über Ihr lokales Netzwerk mit dem Mess-PC verbunden ist.
2. Platzieren Sie den 152Eu-Referenzstandard mit dem einstellbaren Quellenhalter in einem Abstand von etwa 20 cm von der Endkappe des Hochrein-Germanium-Detektors. Zeichnen Sie diese Entfernung auf. Entfernen Sie vor dem Zählvorgang alle Materialien zwischen der Quelle und dem Detektor. Stellen Sie eines der Materialien aus dem Absorber-Kit zwischen die Quelle und den Detektor.
3. Öffnen Sie die Gammaspektroskopiesoftware ProSpect und stellen Sie eine Verbindung zum Lynx II DSA her.
4. Konfigurieren Sie die MCA-Einstellungen wie in Experiment 7 empfohlen.
5. Verwenden Sie die Software, um die empfohlene Detektorvorspannung auf den HPGe-Detektor anzuwenden.
6. Stellen Sie den PHA-Wandlungsgewinn auf 32768-Kanäle ein.
7. Stellen Sie die Grob- und Feinverstärkung des MCA so ein, dass der 1408-keV-Peak im oberen Bereich des Spektrums sichtbar ist.
8. Erfassen Sie die Daten und stellen Sie dabei sicher, dass in mehreren der wichtigsten Peaks im gesamten Spektrum mindestens 10.000 Zählungen erreicht werden. Berechnen Sie mit der Tabelle die Energiekalibrierungskoeffizienten. Geben Sie diese über den Reiter "Energiekalibrierung" in die ProSpect-Software ein.
9. Messen Sie die Netto-Peakfläche und die Unsicherheit für jeden der wichtigsten Peaks. Berechnen Sie das Verhältnis der Zählraten für jeden Peak zu den Zählraten für die in Experiment 8 erhobenen Daten.
10. Modellieren Sie die Experimenteinrichtung von Schritt 2 in LabSOCS Geometry Composer und ermitteln die Effizienzwerte. Berechnen Sie das Verhältnis der Effizienzwerte für diese Geometrie zu den in Übung 1 ermittelten Effizienzwerten. Wie fällt der Vergleich zu den in Schritt 9 berechneten Verhältnissen aus?
Übung 3
1. Legen Sie eine volumetrische Probe unbekannter Aktivität auf den Germanium-Detektor.
2. Zählen Sie die Probe so lange, bis 10 000 Zählungen in mehreren signifikanten Peaks vorliegen. Messen Sie die Netto-Peakfläche und die Unsicherheit für jeden der wichtigsten Peaks und ermitteln die möglichen Nuklide in der Probe.
Suchen Sie mit LabSOCS Geometry Composer eine Vorlage, die mit der Messgeometrie übereinstimmt. Messen Sie die physikalischen Parameter und geben sie in die LabSOCS-Software ein. Ermitteln Sie die Effizienzergebnisse.
4. Berechnen Sie anhand der LabSOCS-Effizienzergebnisse, der Peakflächenzählungen und der bekannten Photonenintensitäten für die infrage kommenden Nuklide die Aktivität der Nuklide in der Probe. Besprechen Sie die möglichen Fehlerquellen und Unsicherheiten.
Übung 4
1. Erstellen Sie in LabSOCS Geometry Composer ein Modell einer volumetrischen Probe (wie z. B. die einfache Becherschablone) auf der Detektorendkappe oder verwenden Sie das aus der vorherigen Übung und berechnen Sie die Effizienz für einen Photonenenergiebereich.
2. Berechnen Sie die Effizienz derselben Probe in Schritt 1, jedoch in einem Abstand von 10 cm vom Detektor.
3. Berechnen Sie die Effizienz derselben Probe in Schritt 1, jedoch in einem Abstand von 10 cm vom Detektor und mit einem Absorber zwischen der Probe und dem Detektor.
4. Vergleichen Sie die drei modellierten Wirkungsgrade mit den beiden gemessenen Wirkungsgraden für einen nieder-, einen mittel- und einen hochenergetischen Peak. Welcher Parameter ist für die verschiedenen Energien am wichtigsten: der Abstand zwischen Quelle und Detektor oder die Materialien zwischen Quelle und Detektor?
5. Verringern Sie in einem der erstellten Modelle die Füllhöhe der Probe um 50 % und berechnen Sie die Wirkungsgrade. Vergleichen Sie diese dann mit dem ursprünglichen Modell für einen hoch-, mittel- und niederenergetischen Peak. Für welche Energie ändert sich die Effizienz am meisten? Erklären Sie das Ergebnis.