Laborversuch 8: Effizienzkalibrierung für Gammaspektrometrie

Zweck:
- Gezeigt werden soll das Verfahren zur Messung der Effizienz (Nachweiswahrscheinlichkeit) eines NaI- und eines HPGe-Detektors als Funktion der Gammaenergie.
- Dieses dient der Einführung des Konzepts der Effizienzkalibrierung.
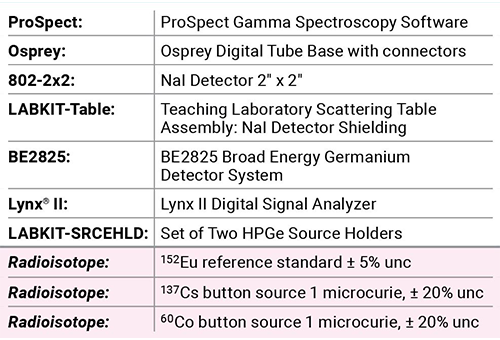
Erforderliches Equipment:
Übersicht über die Theoretie:
Eine radioaktive Quelle emittiert eine bestimmte Anzahl von Photonen (Gammastrahlung) und der Detektor (z. B. ein NaI-Szintillationsdetektor oder ein HPGe-Detektor) wird zum Nachweis dieser Photonen verwendet. Die Anzahl der von der radioaktiven Quelle emittierten Photonen ist immer größer als die Anzahl der vom Detektor nachgewiesenen Photonen. Das Verhältnis der Anzahl der vom Detektor detektierten oder nachgewiesenen Photonen zur Anzahl der von der Quelle emittierten Photonen wird als Detektionseffizienz bezeichnet. Die Detektionseffizienz ε kann wie folgt angegeben werden:

Wobei:
Nmeas für die Anzahl der vom Detektor festgestellten Photonen (Zählungen oder „measure“) steht.
Nemit steht für die Anzahl der von der Quelle emittierten Photonen.
Bei den meisten Anwendungen ist die Peak-Effizienz der Full-Energy-Peaks von Interesse; in diesem Fall ist der Nmeas-Wert die Anzahl der Zählungen im Full-Energy-Peak und Nemit die Anzahl der Photonen, die für diese spezifische Energie emittiert werden.

Abbildung 8-1: Zerfallsschema von 137Cs.
Die Anzahl der im Detektor beobachteten Zählereignisse hängt weitgehend von den Eigenschaften des Detektors wie Größe, Ordnungszahl und Dichte ab. Die Anzahl der festgestellten Zählereignisse hängt ebenfalls von der Aktivität der Quelle, dem Abstand zwischen Quelle und Detektor und den Materialien zwischen Quelle und Detektor ab. Aus der Aktivität der Quelle resultiert die Zerfallsrate der Quelle; die Aktivität wird normalerweise in Einheiten von Becquerel oder Curie ausgedrückt. Ein Becquerel entspricht dem Zerfall von 1 Atomkern pro Sekunde, ein Curie entspricht 3,7 x 1010 radioaktiven Zerfällen pro Sekunde. Für die meisten Kerne entspricht die Anzahl der Photonen, die bei einer bestimmten Energie pro Sekunde emittiert werden, nicht der Anzahl der Zerfälle pro Sekunde, sondern sie liegt in der Regel niedriger. Es kann verschiedene Zerfallspfade im Tochterkern geben, und die relevante Übergangsstrahlung kann von anderen Übergängen umgangen werden. Die Gesamtzahl der bei einem Zerfall emittierten Gammaquanten kann größer als eins sein. Anstelle einer Gammaquantenemission kann ein Kern seine Anregungsenergie auch über andere Prozesse, wie die innere Konversion abgeben. Bei dieser wird die Energie auf ein Hüllenelektron übertragen und die übertragene Energie ist die Bindungsenergie plus der kinetischen Energie des Elektrons Den Parameter, der zur Beschreibung der Anzahl der Gammastrahlen pro Zerfall für eine Gammaenergie verwendet wird nennt man Intensität oder Entkommwahrscheinlichkeit. Die Anzahl der erwarteten Zählereignisse lässt sich wie in Gleichung 8-2 angegeben definieren.

Wobei:
A die Aktivität ist, ausgedrückt in Zerfällen pro Sekunde (oder Bq).
Y ist die Gammastrahlungsentkommwahrscheinlichkeit,
t ist die Zeit in Sekunden.
Die Aktivität der Quelle wird in der Regel in Bezug auf ein bestimmtes Datum angegeben. Für die Aktivität zum Zeitpunkt des Experiments ist anhand von Gleichung 8-3 eine Zerfallskorrektur vorzunehmen.

Wobei:
A die aktuelle Aktivität ist.
A0 die Aktivität zum Referenzdatum.
t die seit dem Referenzdatum verstrichene Zeit.
t1/2 ist die Halbwertszeit des betrachteten Nuklids.
Alle rückführbaren radioaktiven Quellen verfügen über Quellenzertifikate, welche die Quellaktivität für den Referenztag der Zertifizierung in Becquerel oder Curie angibt. Einige Zertifikate geben jedoch die Emissionsrate in Gamma pro Sekunde an, was bedeutet, dass die Entkommwahrscheinlichkeit oder die Intensität in die angegebenen Werte eingerechnet wurde. Dies ist bei gemischten Gamma-Quellen üblich, wie in Tabelle 8-1 gezeigt.
Tabelle 8-1: Typisches Quellenzertifikat für eine gemischte Gammaquelle.

Effizienzen können als absolut, intrinsisch oder relativ bezeichnet werden. Die absolute Effizienz ist das Verhältnis der Gesamtzahl der detektierten Photonen zur Anzahl der von der Quelle emittierten Photonen. Die intrinsische Effizienz ist das Verhältnis der Anzahl der detektierten Photonen zur Anzahl der auf der Detektorfläche einfallenden Photonen. Absolute und intrinsische Effizienzen können als die Peak-Effizienz der Full-Energy-Peaks ausgedrückt werden, bei der nur die Photonen berücksichtigt werden, die in den Full-Energy-Peaks zu Zählereignissen führen. Häufig, speziell bei der Festlegung von Spezifikationen, werden die Germanium-Detektoreffizienzen als relative Effizienzen ausgedrückt. Dabei handelt es sich um die Effizienz im Verhältnis zu einer 60Co-Quelle (unter Verwendung des 1.332-keV-Peaks), die mit einem 3"x3"-NaI(Tl)-Detektor in einem Abstand von 25 cm vom Detektor gemessen wird.

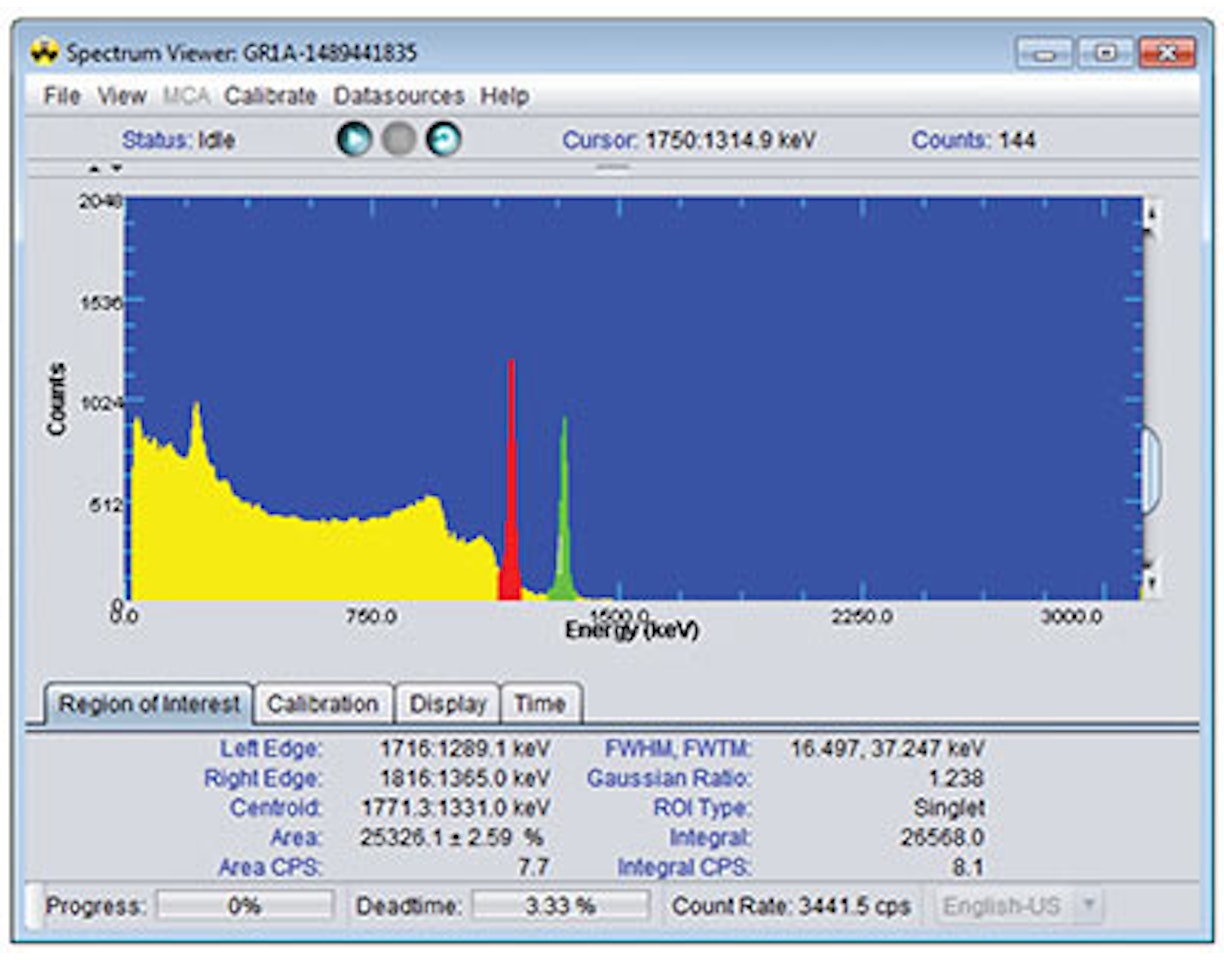
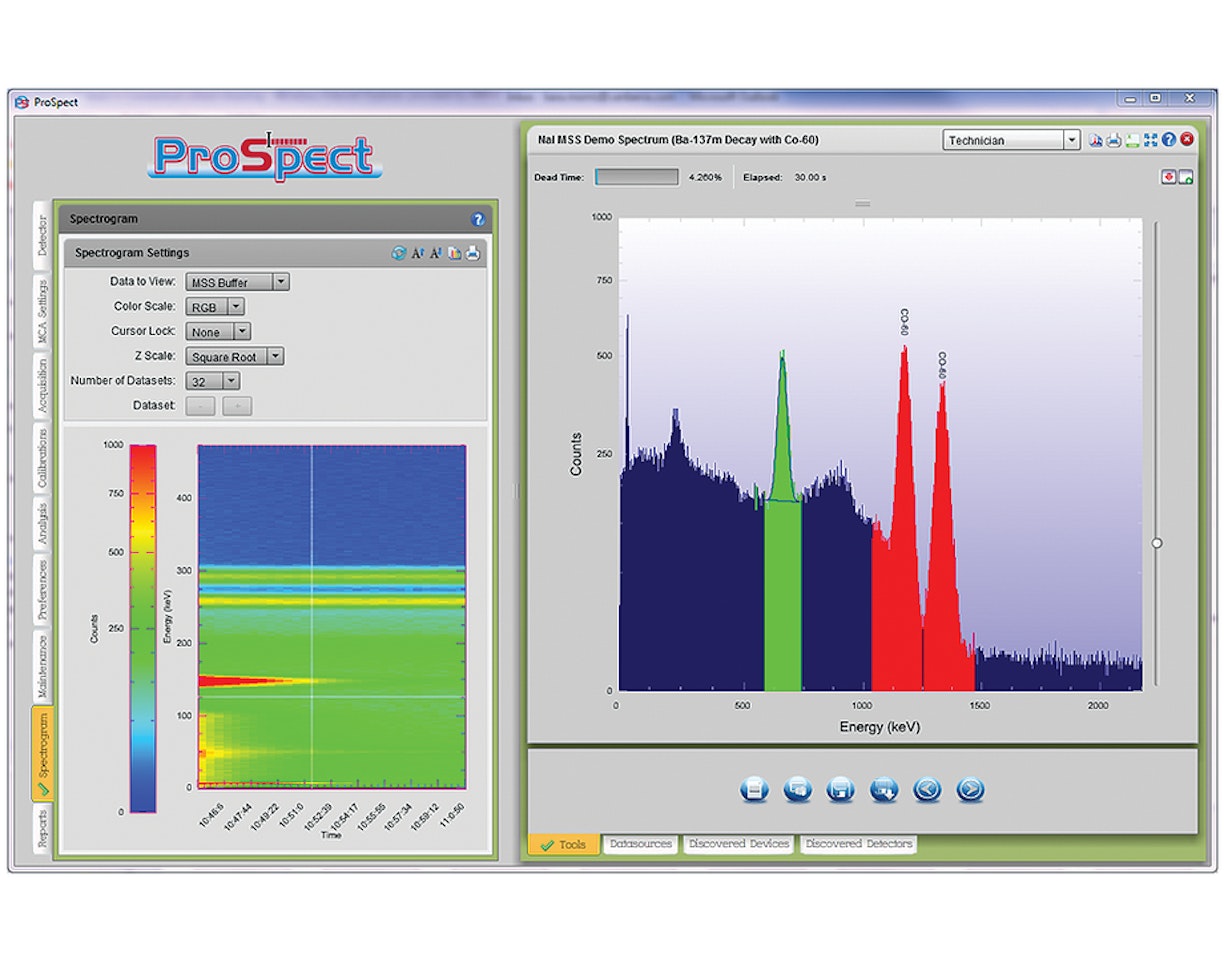
Abbildung 8-2: Typisches NaI-Spektrum für eine gemischte Gammaquelle.
Anleitung für Experiment 8:
Verwendung eines 2"x2"-NaI-Detektors
1. Platzieren Sie den 152Eu-Referenzstandard in einem Abstand von etwa 20 cm von der Oberfläche eines 2"x 2"-NaI-Detektors.
2. Konfigurieren Sie die Vielkanalanalysator-Einstellungen gemäß Anleitung für Experiment 1.
3. Stellen Sie die Grob- und Feinverstärkung des VKA so ein, dass der 1408-keV-Peak im hochenergetischen Bereich des Spektrums sichtbar ist.
4. Erfassen Sie die Daten und stellen Sie dabei sicher, dass in mehreren der wichtigsten Peaks im gesamten Spektrum mindestens 10.000 Zählereignisse erreicht werden. Führen Sie eine Energiekalibrierung durch und beziehen Sie sich dazu gegebenenfalls auf die Anleitung für Experiment 2.
5. Messen Sie die Netto-Peakfläche und die statistische Unsicherheit für jeden der wichtigsten der in der Zertifikatsdatei aufgeführten Peaks. Verwenden Sie für jeden Gammastrahlungs-Peak die Gleichung 8-1, um die Effizienz zu bestimmen. Berechnen Sie weiterhin die Unsicherheit in der Effizienz (verwenden Sie bei Bedarf die Referenz 4 auf Seite 77). Beachten Sie: Wenn für diese Berechnung Zählereignisse (statt Zählereignisse pro Sekunde) verwendet werden sollen (gemäß Gleichung 8-1), sind die Gammaquanten-Emissionsraten in der Zertifikatsdatei zunächst in die Anzahl der während der Messung emittierten Gammastrahlen umzurechnen (durch Multiplikation mit der Messzeit). Die Photonenintensitäten sind in Tabelle 8-2 zur besseren Übersicht angegeben.
Tabelle 8-2: Verzweigungsverhältnisse für die wichtigsten 152Eu-Gammastrahlen.

6. Stellen Sie in Microsoft Excel oder einem anderen Programm die Effizienz (und Unsicherheit) im Verhältnis zur Energie dar. Das Ergebnis sollte ähnlich wie in Abbildung 8-3 aussehen. Kommentieren Sie die Form der Kurve.

Abbildung 8-3: Repräsentative Effizienz des NaI-Detektors als Funktion der Energie.
Verwendung des HPGe-Detektors
Die Bestimmung der Effizienzwerte mit HPGe-Detektoren erfolgt ähnlich wie beim 2"x2"-NaI-Detektor.
Der Hauptunterschied bei den erzielten Ergebnissen besteht darin, dass die Auflösung des HPGe-Detektors viel höher ist als die eines NaI-Detektors. Die typische Auflösung eines HPGe-Detektors beträgt weniger als 0,2 %, die eines NaI-Detektors hingegen etwa 7,5 %.
1. Stellen Sie sicher, dass der Lynx II DSA (mit angeschlossenem HPGe-Detektor) direkt oder über Ihr lokales Netzwerk mit dem Mess-PC verbunden ist.
2. Platzieren Sie den 152Eu-Referenzstandard mit dem einstellbaren Quellenhalter in einem Abstand von etwa 20 cm von der Endkappe des hochreinen Germanium-Detektors. Dokumentieren Sie diese Entfernung. Entfernen Sie vor der Messung die Kunststoffkappe vom Detektor.
3. Öffnen Sie die Gammaspektroskopiesoftware ProSpect und stellen Sie eine Verbindung zum Lynx II DSA her.
4. Konfigurieren Sie den VKA wie in Experiment 7 für einen HPGe-Detektor empfohlen.
5. Legen Sie anhand der Software die empfohlene Detektorhochspannung auf den HPGe-Detektor an.
6. Stellen Sie die Anzahl der Spektrenkanäle auf 32768 ein.
7. Stellen Sie die Grob- und Feinverstärkung des VKA so ein, dass der 1408-keV-Peak im oberen Bereich des Spektrums sichtbar ist.
8. Messen Sie ein Spektrum und stellen Sie dabei sicher, dass in mehreren der wichtigsten Peaks im gesamten Spektrum mindestens 10.000 Zählereignisse erreicht werden. Nehmen Sie die Energiekalibrierung des Systems vor und orientieren Sie sich dazu bei Bedarf an Experiment 1.
9. Messen Sie die Netto-Peakfläche und die statistische Unsicherheit für jeden der wichtigsten der in Tabelle 8-2 aufgeführten Peaks. Verwenden Sie für jeden Full-Energy-Peak die Gleichung 8-1, um die Effizienz zu bestimmen. Berechnen Sie weiterhin die Unsicherheit in der Effizienz (verwenden Sie bei Bedarf die Referenz 4 auf Seite 77). Beachten Sie: Wenn für diese Berechnung Zählereignisse (statt Zählereignisse pro Sekunde) verwendet werden sollen (gemäß Gleichung 8-1), sind die Gammaquanten-Emissionsraten in der Zertifikatsdatei zunächst in die Anzahl der während der Messung emittierten Gammastrahlen umzurechnen (durch Multiplikation mit der Messzeit). Die Photonenintensitäten sind in Tabelle 8-2 zur besseren Übersicht angegeben.
10. Stellen Sie in Microsoft Excel oder einem anderen Programm die Effizienz (und Unsicherheit) im Verhältnis zur Energie dar. Vergleichen Sie die Ergebnisse mit der aus der NaI-Messung ermittelten Effizienz.
11. Entfernen Sie den 152Eu-Referenzstandard und ersetzen Sie ihn im gleichen Abstand durch die 60Co-Quelle. Zählen Sie, bis in jedem der beiden Primärpeaks mindestens 10.000 Zählungen erreicht sind. Bestimmen Sie mit den Gleichungen 8-2 und 8-3 und durch Interpolation mit der in Schritt 10 berechneten Effizienzkurve die Aktivität der 60Co-Quelle. Welche Werte werden im Vergleich zum 60Co-Quellenzertifikat ermittelt?
12. Wiederholen Sie Schritt 11 mit der 137Cs-Quelle. Welcher Wert wird im Vergleich zur Aktivität auf dem Quellenzertifikat ermittelt?
13. Wählen Sie eine der Quellen und platzieren Sie diese in einem Abstand erst von 10 cm und dann von 25 cm. Messen Sie für jede Position, bis etwa 10.000 Zählereignisse in den Primärpeaks erreicht sind. Berechnen Sie die Effizienzkurve für jede Geometrie. Was stellt man beim Vergleich fest? Geht daraus hervor, dass die Effizienz proportional zum Kehrwert des Quadrats des Abstands ist?